R C Circuit Transient Analysis

Transient Analysis 

Transients are generated in electrical circuits having energy storage elements like inductors or capacitors when sudden changes occur in the operating conditions. This occurs when the circuit is powered up for the first time. A first order circuit has a single energy storage element for example either a capacitor or an inductor. A second order circuit has two storage elements for example both an inductor and a capacitor.

R C Circuit Transient Analysis
Consider the circuit shown in FIG. 1 below:

FIG. 1: Circuit with Series Resistor and Capacitor

Using to Kirchhoff's Voltage Law (KVL) which states the voltage around a loop equals the sum of 
every voltage drop in the same loop. Referring to FIG. 1 it can be said:
V = VR(t) + Vc(t)...........equation (1)

For a capacitor:
Vc(t) = 1/C∫i(t)dt or
dVc(t)/dt = 1/C i(t)
1/C i(t) = dVc(t)/dt
i(t) = C(dVc(t)/dt)..........equation (2)

In this circuit the current that flows through capacitor C also flows through resistor R.
So VR(t) = R i(t) or
VR(t) = RC(dVc(t)/dt)
Equation (1) can be rewritten as:
V = RC(dVc(t)/dt) + Vc(t)
RC(dVc(t)/dt) = V – Vc(t)
RC dVc(t) = (V – Vc(t))dt
RC dVc(t)/(V – Vc(t)) = dt
-RC ln (V – Vc(t)) = t + k.......equation (3)

To determine k a starting condition must be considered. Initially the switch is open and the voltage across the capacitor is zero. Thus at t=0, Vc(t)=0. Replacing these values in equation (3) it can be said that:
-RC ln V = k or
k = -RC ln V............equation (4)

Now substitute the value of k in equation (4) in equation (3):
-RC ln (V – Vc(t)) = t -RC ln V
-RC ln (V – Vc(t)) + RC ln V = t
-RC ((ln (V – Vc(t)) - ln V) = t
ln (V – Vc(t)) – ln V = -t/RC
ln ((V – Vc(t))/V) = -t/RC
Taking the anti-log on both sides
(V – Vc(t))/V = EXP(-t/RC)
V – Vc(t) = V(EXP(-t/RC))
– Vc(t) = V(EXP(-t/RC) – V
Vc(t) = V – V(EXP(-t/RC)
Vc(t) = V(1 – EXP(-t/RC))............equation (5)
Equation (5) is the voltage across the capacitor in relation to time.

From equation (1) that is V = VR(t) + Vc(t) it can be said that:
VR(t) = V – Vc(t)................equation (6)

From equation (5) that is Vc(t) = V(1 – EXP(-t/RC)) or Vc(t) = V – V(EXP(-t/RC))
Equation (6) can be re-written as:
VR(t) = V – V + V(EXP(-t/RC))
VR(t) = V(EXP(-t/RC))..................equation (7)

The current i(t) can be written as:
i(t) = (VR(t))/R

But VR(t) = V(EXP(-t/RC))
i(t) = (V(EXP(-t/RC)))/R
i(t) = (V/R)EXP(-t/RC).............equation (8)

The RC time constant, also called tau or τ, the time constant (in seconds) of an RC circuit, is equal to the product of the circuit resistance (in ohms) and the circuit capacitance (in farads).
τ =RC (seconds)
So after one time constant τ = 1xRC = RC
Vc(RC) = V(1 – EXP(-RC/RC)) = V(1 – EXP(-1)) = V (1 – 0.3679) = V(0.6321) = 0.6321V
VR(RC) = V(EXP(-RC/RC)) = V(EXP(-1) = V(0.3679) = 0.3679V
i(RC) = (V/R)EXP(-t/RC) = (V/R)EXP(-RC/RC) = (V/R)EXP(-1) = (V/R)(0.3679) = 0.3679(V/R).

After five time constants τ = 5xRC = 5RC
Vc(5RC) = V(1 – EXP(-5RC/RC)) = V(1 – EXP(-5)) = V (1 – 0.0067) = V(0.9933) = 0.9933V
VR(5RC) = V(EXP(-5RC/RC)) = V(EXP(-5)) = V(0.0067) = 0.0067V
i(5RC) = (V/R)EXP(-t/RC) = (V/R)EXP(-5RC/RC) = (V/R)EXP(-5) = (V/R)(0.0067) = 0.0067(V/R).

FIG. 2: VC(t) and VR(t) as a Function of Time in Time Constants

Shown below is the circuit current i(t) as a function of time in time constants.

FIG. 3: I(t) as a Function of Time in Time Constants

A simulation was done in LTspice. The resistor R1 was chosen as 10 000Ω. The capacitor C1 was chosen as 100uF. This gives a time constant of τ= R x C = 10 000Ω x 100uF = 1 second. The input pulse starts at 0V, rises to 1V, has a delay of 0.1s, a rise time of 0.01s, a fall time of 0.01s, an on time of 5s, a period of 10s and the cycle is repeated 3 times. The simulation was run for 20 seconds. The circuit is shown in figure 4 below.

FIG. 4: Circuit Simulated in LTspice.

Measurements were made which are shown in figure 5 below. The read trace is the input pulse. The green trace is the voltage across resistor R1. The blue trace is the voltage across the capacitor C1.

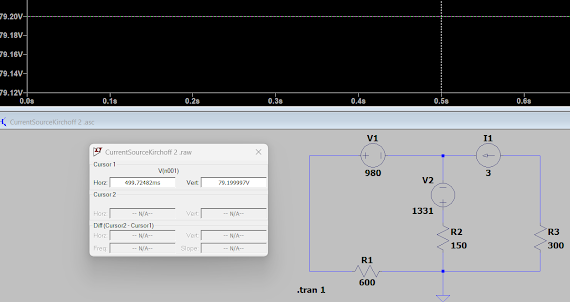
FIG. 5: Traces Input Voltage-Red, R1-Green, and C1-Blue Simulated in LTspice.

Shown in FIG. 6 below is the input voltage indicate by the blue trace and the current in R1 is shown by the green trace.

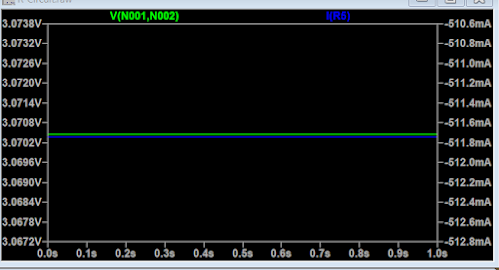
FIG. 6: Traces Input Voltage-Blue and R1 Current-Green Simulated in LTspice.

There is some resemblance between the resistor calculated voltage and current and capacitor voltage and that of the values obtained by the LTspice simulation.

Solving Circuit Having a Current Source with Kirchhoff’s Law

 We are given the particulars in the circuit below in FIG. 1 and asked to calculate E₂.

FIG. 1: Circuit Having a Current Source

The voltage drop across resistor R₁=600Ω is given as 80V. Thus, using Ohm’s law of I=V/R the current flowing in R₁ can be calculated. The current flowing through R₁ is chosen to be I₂ in the circuit above.

I₂ = 80V/600Ω

   = 0,13A

Kirchhoff’s current law (KCL) which states:

“…total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node.“

Using KCL and the currents chosen and indicated in the circuit it can be said that:

I₃ + I₂ = I₁

I₃ = I₁ – I₂, I₂ was calculated as 0,16A and I₁ is given as 3A.

   = 3A-0,13A

   = 2,87A

I₃ = 2,87A

Kirchhoff’s voltage law (KVL) which states:

“…in any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop,”

Using (KVL) it can be stated that:

E₂ = I₃R₂ + I₁R₃

     = (2,87A)(150Ω) + (3A)(300Ω)

      = 431V + 900V

      = 1 331V

Therefore E₂ = 1 331V.

E₁ = 80V-(I3)(R2)

E₁ = 80V - (I₃)(150Ω) + 1 331V

     = 80V - (2,87A)(150Ω) + 1 331V

= 80V - 431V + 1 331V

= 980V

Therefore E₁ = 980V.

What we will do next is implement our circuit in LTspice and check if it is correct. Shown in FIG. 2 below is FIG. 1 implemented in LTspice.

FIG. 2: LTspice Circuit

So, we are working backwards so to speak. We have set V1 which is our E₁. We calculated it to be = 980V so that V1=980V. We also have set V2 which is our E₂ which we calculated to be = 1331V so that V2=1331V. Now we are going to make measurements to see if it complies with what we were originally given.

FIG. 3: Voltage Across Resistor R1 = 79.19999V

As can be seen in FIG. 3 the voltage across according to LTspice is R1 = 79.199999V. This compares well with the 80V we were initially given. Let’s now measure the current in R1 according to LTspice shown in FIG. 4 below.

FIG. 4: Current in Resistor R1 = 132mA.

As can be seen in FIG. 4 the current in R4 according to LTspice is 132mA. This compares well with our previous calculation of I₂ = 80V/600Ω  = 0,13A. Let’s measure the current I₃ according to LTspice which is the current flowing through resistor R2.

FIG. 5: Current in Resistor R2 = 2.868A

As can be seen in FIG. 5 the current in resistor R2 according to the LTspice simulation is 2.868A. According to FIG. 1, the current is I₃. We calculated that to be 2.87A which compares well with LTspice’s calculations.

 

Circuit With One Series and Three Parallel Resistors.

The following circuit and values as shown in figure 1 below are provided. We want to solve this circuit. In particular, the currents in the parallel resistors have to be determined.

FIG. 1: Circuit with One Series and Three Parallel Resistors.

The following values are given: V1=10V, R1=200Ω, R2=300Ω, R3=400Ω, and R4=100Ω.
Let's start with resistors R1, R2, and R3 and determine an equivalent value ReqR1R2R3 for them.
Since R1, R2, and R3 are in parallel we can say:
1/ ReqR1R2R3  = 1/ R1 + 1/ R2 + 1/ R3
                       = 1/200Ω + 1/300Ω + 1/400Ω
                       = 5.0x10^-3(1/Ω) + 3.33x10^-3(1/Ω) + 2.50x10^-3(1/Ω)
                       = 10.83x10^-3(1/Ω)
Thus ReqR1R2R3 = 92.31Ω.
We can now redraw the circuit by replacing R1, R2, and R3 with ReqR1R2R3 as follows:

FIG. 2: Circuit with R₁, R₂, and R₃ Replaced with R_eqR1R2R3.

As R₄ and R_eqR1R2R3 are in series to determine the total resistance of the circuit R_tot we simply add R₄ and R_eqR1R2R3.

Thus, it can be said that:
Rtot = R4 + ReqR1R2R3
       = 100Ω + 92.31Ω
Rtot = 192.31Ω

Now to calculate the total current in the circuit Itot it can be said that:
Itot = V1/Rtot
      = 10V/192.31Ω
      = 52.00x10^-3A
Or it can be said that Itot = 52mA.

 

FIG. 3: Circuit with I_tot=52mA. 

The I_tot = 52mA also flows through resistor R_eqR1R2R3. So, we can calculate the voltage drop across R_eqR1R2R3, V_eqR1R2R3.

VeqR1R2R3 = Itot x ReqR1R2R3
                  = 52mA x 92.31Ω
                  = 52x10-3A x 92.31
                  = 4.8V
VeqR1R2R3 = 4.8V

But remember VeqR1R2R3 is also the voltage drop across resistors R1=200Ω, R2=300Ω, and R3=400Ω as they make up ReqR1R2R3 = 92.31Ω. So, the current in resistors in resistors R1, R2, and R3=400Ω can be calculated as follows:
IR1 = VeqR1R2R3/R1 = 4.8V/200Ω = 24x10-3A or = 24mA.
IR2 = VeqR1R2R3/R2 = 4.8V/300Ω = 16x10-3A or = 16mA.
IR3 = VeqR1R2R3/R3 = 4.8V/400Ω = 12x10-3A or = 12mA.

Itot = IR1 + IR1 + IR3
     = 24mA + 16mA + 12mA
     = 52mA.

This is correct and complies with our previous calculation of Itot=52mA.

FIG. 4: Circuit with I_tot=52mA, I_R1=24mA, I_R2=16mA, I_R3=12mA, and Veq_R1R2R3=4.8V.

The voltage drop across the resistor R4, VR4can now be calculated as follows:

VR4  =10V-VeqR1R2R3
        = 10V-4.8V
        = 5.2V
VR4 = 5.2V

This circuit was also implemented in LTspice. See figure 5 below:

FIG. 5: Circuit Implemented in LTspice.

The current measured in R₄ in LTspice is as shown in figure 6 below:

FIG. 6: Current in R_4, IR4=52mA Measured in LTspice.

Shown in figure 6, the current in resistor R₄, I_R4=52mA as measured in LTspice. This is the same as I_tot=52mA calculated above.

The current measured in resistor R₁ in LTspice is shown in figure 7 below:

FIG. 7: Current in R_1, IR1=24mA Measured in LTspice.

Shown in figure 7, the current in R₁, I_R1=24mA as measured in LTspice. This is the same as I_R1=24mA calculated above.

The current measured in R₂ in LTspice is shown in figure 8 below:

FIG. 8: Current in R2, IR2=16mA Measured in LTspice.

Shown in figure 8, the current in R₂, I_R2=16mA as measured in LTspice. This is the same as I_R2=16mA calculated above.

The current measured in R₃ in LTspice is shown in figure 9 below:

FIG. 9: Current in R_3, IR3=12mA Measured in LTspice.

Shown in figure 9, the current in R₃, I_R3=12mA as measured in LTspice. This is the same as I_R3=12mA calculated above.

Voltage measured across R₁, R₂, and R₃, Veq_R1R2R3 in LTspice shown in figure 10 below:

FIG. 10: Voltage across R₁, R₂, and  R₃, Veq_R1R2R3=4.8V Measured in LTspice.

 Shown in figure 10 above, the voltage across R₁, R₂, and  R₃, Veq_R1R2R3=4.8V as measured in LTspice. It is the same as Veq_R1R2R3=4.8V calculated previously.

 

Circuit With Series and Parallel Resistors

The following circuit shown in figure 1 below has the following values: R1=6.5Ω, R2=4Ω, R3=8Ω, R4=5Ω, and R5=6Ω. The voltage is given as V1=9V. We want to solve the circuit and determine the voltage drop across R5 as well as the current flowing in R5.

FIG. 1: Circuit to be Solved.

Let’s start with resistors R2 and R3 and determine an equivalent value ReqR2R3 for resistors R2 and R3. Since R2 and R3 are in parallel we can say:

1/ ReqR2R3 = 1/R2+1/R3

                  = 1/4Ω+1/8Ω

                  = 0,25(1/Ω) + 0,125(1/Ω)

1/ ReqR2R3 = 0,375(1/Ω).

Rounded off to first two digits: ReqR2R3 = 2,67Ω.

We can now redraw the circuit by replacing R2 and R3 with ReqR2R3 as follows as shown in figure 2 below:

FIG. 2: Circuit Redraw with ReqR2R3.

As ReqR2R3 and R4 are in series we can determine the equivalent resistance for ReqR2R3 and R4, which is indicated as ReqR2R3R4. Thus for resistors ReqR2R3 and R4 in series:

ReqR2R3R4 = ReqR2R3 + R4 

                  = 2,67Ω + 5Ω

                  = 7,67Ω

ReqR2R3R4 = 7,67Ω.

The circuit can thus be redrawn by replacing ReqR2R3 and R4 with ReqR2R3R4 as shown in figure 3 below:

FIG. 3: Circuit Redraw with ReqR2R3R4.

Now what must be obtained is the equivalent resistor ReqR2R3R4R5 for resistors ReqR2R3R4 and R5.

As they are in parallel it can be said that:

1/ReqR2R3R4R5 = 1/ ReqR2R3R4 + 1/R5 

                     = 1/(7,67Ω) + 1/(6Ω)

                      = 1/(7,67)(1/Ω) + 1/6(1/Ω)

      = (1/(7,67) + 1/6)(1/Ω)

      = (0,13 +0,17) (1/Ω)

                      = 0,30(1/Ω).

Or we can say ReqR2R3R4R5 = 3,33Ω.

We can now once again redraw the circuit by replacing resistors ReqR2R3 and R5 with equivalent resistor ReqR2R3R4R5 as shown in figure 4 below:

FIG. 4: Circuit Redraw with ReqR2R3R4R5.

We now have a much-simplified circuit with two series resistors ReqR2R3R4R5=3,33Ω, R1=6,5Ω and a voltage source V1=9V. To calculate the current in the circuit, shown in figure 4, Icircuit, and also flowing through ReqR2R3R4R5 and R1 we can say:
Icircuit = V1/(ReqR2R3R4R5+R1 )
            = 9V/(3,33Ω+6,5Ω)
            =9V/9,83Ω
            = 0,92A
Therefore, Icircuit is equal to 0,92A. Now we can calculate the voltage across ReqR2R3R4R5 which is 
VReqR2R3R4R5.
VReqR2R3R4R5 = (Icircuit)(ReqR2R3R4R5)
                        = (0,92A)(3,33Ω)
                        = 3,06V.

Thus VReqR2R3R4R5 = 3,06V
Referring to figure 3 ReqR2R3R4R5 is in fact ReqR2R3R4 and R5 in parallel. Thus, VReqR2R3R4R5 is also the voltage across R5. Thus VReqR2R3R4R5 is also the voltage drop across R5 that being VR5, thus VR5=3,06V. The current through R5, IR5 can be calculated as follows:
IR5 = VR5/(R5 )
      = 3,06V/(6Ω )
      = 0,51A

Thus IR5=0,51A.

Figure 1 was simulated on LTspice. Measurements were made during the simulation in LTspice of the voltage drop VR5 and current IR5 in resistor R5 and the results are shown in figure 5 below:

FIG. 5: Measurements of IR5 and VR5 Made During LTspice Simulation.

As can be seen in figure 5 the measurement of IR5=-0,5117A, indicated in blue, and VR5=3,0705V, indicated in green, during the simulation of the circuit in figure 1 in LTspice. Don't worry about the (-) in IR5. This is purely due to the chosen measurement convention. This compares well with the calculated values of IR5=0,51A and VR5=3,06V.